写的挺好的，但是源网站在手机上没法看，复制一下放到这里。
目录:
1. 前言
2. 正文
2.1 梯度
2.2 梯度下降算法
2.2.1 批量梯度下降算法
2.2.2 随机梯度下降算法
3.参考文献
1.前言
这篇随笔,记录的是个人对于梯度算法的些许理解. 由于充斥着太多关于梯度算法的各种说明软文,所以呢?
本文是从一个实例出发,来逐步使用各种算法进行求解,并顺便试图将每一种算法,按照自己的理解来阐述一遍.
好了 , 让我们愉快的开始吧~~~~~~~~
注: 本文的核心思想主要是基于在斯坦福cs299的讲义上.
2 正文
为了不显得阐述过于唐突,我们还是简单的对我们要说明的对象进行描绘一下吧~.
我们说的梯度算法 ,又称最速下降法 ,可以从它的名称中看出来,它就是用来快速寻找下降方向的(在数学上又叫做局部极小值).至于为什么叫做梯度算法,
是因为其中使用到了梯度来计算其下降的方向,首先阐述一下梯度吧~
2.1 梯度
梯度: 是表示模型或者函数在某个点的位置法向量,所以它的方向表示下降最快或者上升最快也就很好理解了~
,
如果想对梯度定义有更加细致的了解,可以去看看大学微积分相关课程吧
我们先通过这样一个简单的平面来对梯度进行说明: ax+by+c=0求解:我们可以求解（通过对x,y求解偏导数）它的法向量为(a,b),由于是一个平面所以法向量
是固定的,但是如果我们将这个平面掰歪,使其成为一个曲面呢? (函数如下图)
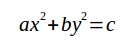
我们可以求解(通过对方程进行偏导数,其实就是(2ax,2by),由于是曲面,所以发现的方向也是随着(x,y)坐标而改变的. 然后我们不妨
在回来看一下梯度的定义: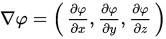 
可以发现上面的那个求解方式,其实和梯度求解的方式是一样的.(详情可以去查阅梯度的wiki),说完了梯度之后,我们来进一步说一下
梯度算法使如何使用到梯度(grad)来进行快速下降或者上升的吧.
2.2 梯度下降算法
为了更好的说明梯度下降算法,首先我们来看看下面这个例子吧~
我们使用Rosenbrock函数,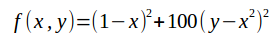
使用梯度下降法来求解它的最小值(也就是如何能够快速的进入跑到谷底).
首先展示一下该函数的模型:
该模型的代码:
# -*- coding: utf-8 -*-
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import animation as amat
"this function: f(x,y) = (1-x)^2 + 100*(y - x^2)^2"
def Rosenbrock(x, y):
return np.power(1 - x, 2) + np.power(100 * (y - np.power(x, 2)), 2)
def show(X, Y, func=Rosenbrock):
fig = plt.figure()
ax = Axes3D(fig)
X, Y = np.meshgrid(X, Y, sparse=True)
Z = func(X, Y)
plt.title("gradeAscent image")
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow', )
ax.set_xlabel('x label', color='r')
ax.set_ylabel('y label', color='g')
ax.set_zlabel('z label', color='b')
amat.FuncAnimation(fig, Rosenbrock, frames=200, interval=20, blit=True)
plt.show()
if __name__ == '__main__':
X = np.arange(-2, 2, 0.1)
Y = np.arange(-2, 2, 0.1)
Z = Rosenbrock(X, Y)
show(X, Y, Rosenbrock)
我们求解出它的梯度方向grad(f(x,y)) = ( -2*( 1 - x ) -400( y - x*x )*x , 200( y - x*x ) )沿着该梯度的反方向就可以快速确定x,y位置的最小点.
即最小值 f(1,1)min = 0
效果图1:
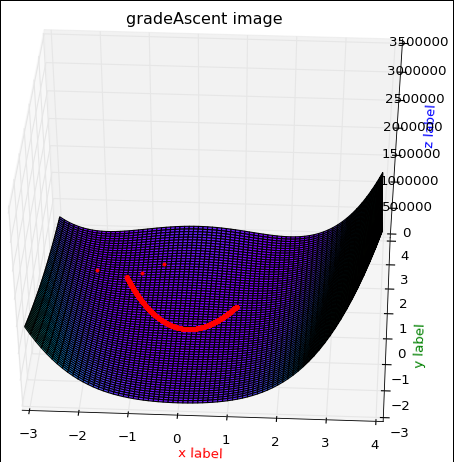
数据变化1:
效果图2:
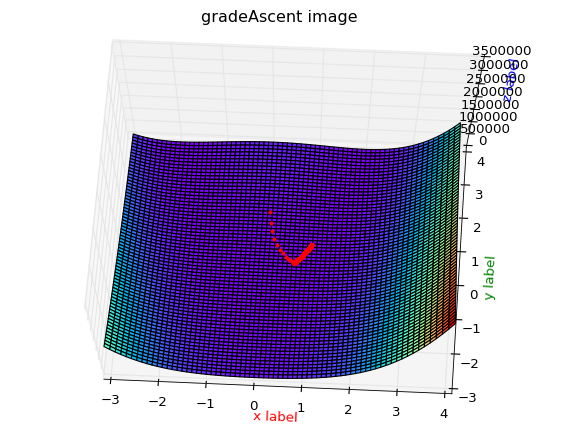
数据变化截图:
附上这部分代码:
# -*- coding: utf-8 -*-
import random
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import animation as amat
"this function: f(x,y) = (1-x)^2 + 100*(y - x^2)^2"
def Rosenbrock(x, y):
return np.power(1 - x, 2) + np.power(100 * (y - np.power(x, 2)), 2)
def show(X, Y, func=Rosenbrock):
fig = plt.figure()
ax = Axes3D(fig)
X, Y = np.meshgrid(X, Y, sparse=True)
Z = func(X, Y)
plt.title("gradeAscent image")
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow', )
ax.set_xlabel('x label', color='r')
ax.set_ylabel('y label', color='g')
ax.set_zlabel('z label', color='b')
plt.show()
def drawPaht(px, py, pz, X, Y, func=Rosenbrock):
fig = plt.figure()
ax = Axes3D(fig)
X, Y = np.meshgrid(X, Y, sparse=True)
Z = func(X, Y)
plt.title("gradeAscent image")
ax.set_xlabel('x label', color='r')
ax.set_ylabel('y label', color='g')
ax.set_zlabel('z label', color='b')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow', )
ax.plot(px, py, pz, 'r.') # 绘点
plt.show()
def gradeAscent(X, Y, Maxcycles=10000, learnRate=0.0008):
# x, Y = np.meshgrid(X, Y, sparse=True)
new_x = [X]
new_Y = [Y]
g_z=[Rosenbrock(X, Y)]
current_x = X
current_Y = Y
for cycle in range(Maxcycles):
"为了更好的表示grad,我这里对表达式不进行化解"
current_Y -= learnRate * 200 * (Y - X * X)
current_x -= learnRate * (-2 * (1 - X) - 400 * X * (Y - X * X))
X = current_x
Y = current_Y
new_x.append(X)
new_Y.append(Y)
g_z.append(Rosenbrock(X, Y))
return new_x, new_Y, g_z
if __name__ == '__main__':
X = np.arange(-3, 4, 0.1)
Y = np.arange(-3, 4, 0.1)
x = random.uniform(-3, 4)
y = random.uniform(-3, 4)
print x,y
x, y, z = gradeAscent(x, y)
print len(x),x
print len(y),y
print len(z),z
drawPaht(x, y, z, X, Y, Rosenbrock)
如上题,在数学上,我们使用梯度可以无限的逼近函数的最小点.但是在工业上呢? 我们如何对一些一个数据集进行处理呢?
很明显的思路是将其转化成一个函数,打比赛的时候,面对这些数据,我们会使用生成函数方式来构造一个,我们称之为生成函数,或者母函数或者其他吧~,但是
电脑面对这一滩数据的时候,通常是这样的
所以还是需要我们手动给予一个通用表达式,比如线性的我们需要设定它为y=kx+b,然后在给电脑这些数据,告诉它说,这些个数据是线性相关的,
你去找到一个k,b是这些点尽可能的满足这个方程吧!,而这个过程我们又将它称之为拟合过程.
所以呢? 面对一滩数据,而我们给定了一个通用的表达式比如:
其中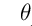
为每一个特征变量的权重,比如特征X1的权重为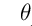1,,我们设定x0=1,然后我们将其简化为:
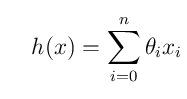
如果我们在将其转化成多维空间的话,其实可以使用还可以这样:
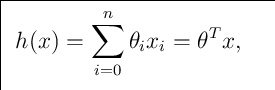
但是到这里,这里依旧还只是一个通试而已,那么我们该如何使用其那些数据呢?
这时候,我们需要来引入一个新的函数,来评估这个通式(我们可以随机给这个式子权重赋值)与实际的值是否在可接收的范围!~
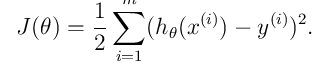
这个函数称谓有两种,一种是损失函数(Loss function),一种是误差函数(Error function),我们在这里就称它为损失函数好了,
说明一下这个式子的含义:
J表示给定的函数预测值和实际值Y的均方差,它反映的是预测值与实际值的一个偏离的程度. 但我们说完这些,再结合上面的那个题,
那么我们是否就想到点什么?
是的我们是否可以用梯度下降算法来快速的无限逼近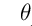,使得J达到最小,当J达到最小的时候,那么我们这个时候的
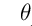,不就是无限接近真是且理想的的那个权重
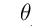么?
然后我们再按照梯度的方向逐步的移动,慢慢的逼近收敛值.用表达式表示为:
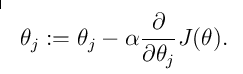
其中需要说明的是:
阿尔法表示的一个学习率,之所以添加这个学习率,是因为我们使用的是均方差,如果我们随机的方程预测的值与实际的值偏差比较大的话,
均方差的值将会非常巨大,这样的话,可能造成我们的这个损失函数出现大幅度的偏移，我们称之为摆钟行为,所以为了避免出现这种情况,这个值就这么的诞生了,这个值的大小,
可以用来调整我们移动的的步子大小,不要调的太大(一般设定在0.0001),当然也应场景而定哈~,还需要解释的是:
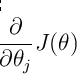表示的是损失函数的权重梯度,那么对于这个梯度,化简为:
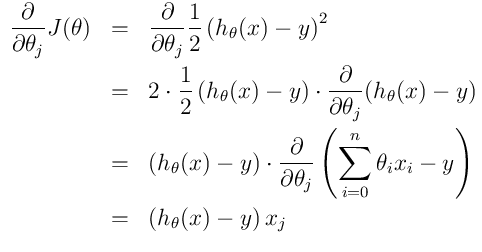
2.2.1 批量梯度下降算法(BGD)
得到上面的推倒之后, 所以我们可以用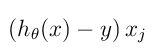
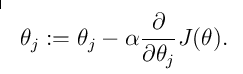,替换掉中的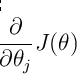,然后我们将会得到这样一个方程:
,解释一下这个方程吧~:
如何去理解这个方程中的i,j,恩,下标j其实就是我们的对应的第j个权重,i表示的是样本数据中第i组训练数据,如果还迷糊的话,我们用一点伪代码来表示一下吧:
"这里权重用W表示 , trainingSet 表示训练数据集合 "for i in range(len(trainingSet)): "n 表示有多少个特征Xj (j属于[1,n])" for j in range(n): w -= a*(yi - h(xi))Xij
而这种方式,是将所有的样本M都参与进去训练,然后得到一个权重值w.这种方式,我们称之为批量梯度下降算法,也就是BGD. 是的,看看吧,
其实并不是很难懂对吧~.
但是这个算法有个缺点,我们算法时间复杂度为O(n^2),当样本量比较大的话,计算量就会变得很大,所以这种方式适用的范围,仅是对那些样本较小的数据而言,
对于大数据量样本而言,这个还是不太好的.那么有没有时间复杂度比O(n^2)低一点的算法呢,? 是有的
2.2.2 随机梯度下降算法(SGD)
随机梯度下降算法,这个介绍起来就不那么好统一了,但是它的大体思路就是: 在给定的样本集合M中,随机取出副本N代替原始样本M来作为全集,对模型进行训练.这种训练由于是抽取部分数据,所以有较大的几率得到的是,一个局部最优解.但是一个明显的好处是,如果在样本抽取合适范围内,既会求出结果,而且速度还快.对于随机梯度下降算法的各种变种,详情请看这篇博客>An overview of gradient descent optimization algorithms.
3.参考文献:
http://sebastianruder.com/optimizing-gradient-descent/index.html各种随机梯度算法变种.
http://cs229.stanford.edu/materials.html 斯坦福机器学习讲义第一章.
发表评论:
◎欢迎参与讨论，请在这里发表您的看法、交流您的观点。